不同分蘖、叶数及部位的小麦叶面积变化的研究
在以大田小麦群体为对象进行生长分析研究过程中,需要一种简单、迅速、准确测定小麦群体叶面积的方法。为了寻求一种简单适用的方法,首先需要了解小麦叶面积的变异规律。本文是三年研究的结果:随着典位的增高,各羹位的总叶面积或单叶平均面积都相应降低。任一葵位的叶片,都是随着叶位的增高而叶面积逐次加大,但抽穗后,全部叶片伸展开,叶面积扫描仪扫描叶面积大小发现:大多数蘖位是以倒数第二叶片面积最大,少数是旗叶最大。不同时期的各典位上的叶片,以倒二叶的面积相对稳定。不同粟位比较则以主茎上的倒二叶变异系数最小。不同孽位相比,以主茎倒二、三两叶的平均面积与单株叶片总面积相关系数最大(r=0.91和r=0.82)。用三个品种,三个时期的资料求出理论叶面积的回归方程和三个品种综合计算的回归方程(显著性均为P<0.05 )。用国内外引进的不同株型的稀播材料检验所得回归方程的适用性,发现分孽力强的品种在营养面积大的情况下,所求回归方程式不适用,对这类情况用经验方法找出了校正值的计算方法。可以根据回归方程和校正值,编制出小麦叶面积查算表。
早在本世纪初,布莱克曼注意到植物重量的增长与其已有的重量成比例,在生长期间重量呈指数增加。据此布莱克曼提出“效率指数”的概念;并引用凯尔文的“复利定理描述植物的生长。布里格斯及凯得等人发展了上述概念并提供了近似生长分析的典型基础。在这个过程中形成了生长的定义为“相对生长率”,即叶面积比例和单位叶面积光合率(以后称为净同化率)的相乘积。随着生长分析研究工作的发展,植物生理学和作物栽培学等工作者进行了作物群体的生长分析研究。我国在六十年代也开展了大量的有关水稻和小麦的群体研究。这些研究得力于沃森提出的“叶面积系数”(LAI)的概念。沃森指出,有关植物干物质积累的测定是LAI和它工作时间的积分。根据这个概念,在六十年代初期,对于光射入和光竞争进行了大量的研究工作。这些间题涉及到找出群幕配置,叶序及叶位角度在不同光度条件下最适宜的LAI。当前在高光效育种工作中也多致力于根据LAI/叶角关系,来培育高光效的品种。我们在六十年代的小麦群体研究和七十年代小麦高产栽培的研究中,认识到小麦生物学产量的高低,在较大程度上取决于叶面积的大小、叶片功效期的长短和单位叶面积光合生产率的高低。在正常情况下,某一品种在某一地区的叶片功能期是相对稳定的;这样叶面积的大小和光合生产率的高低,显然就成为干物质积累的决定因素。因此在小麦的各生育阶段,准确而迅速地估算出小麦群体的叶面积系数便成为进行生长分析不可缺少的基本工作;也是在生产上衡量小麦生长状况,制定栽培措施十分重要的依据指标。在上述研究工作中,我们曾用打孔、称量法以及求积仪法等估算小麦的叶面积,深感这些方法手续繁杂,工作量很大,不利于及时测定。为了解决这一问题,我们试图设计一种小麦叶面积查算表,以求简化手续。减少工作量。因而首先需要研究小麦叶片面积的变异规律,找出代表性最强,面积稳定的叶片,再据以推算整个群体的叶面积指数。本文就是这项研究的报告。
材料和方法
1963年在太谷山西农学院实习农场用品种农大183;1974年在晋南闻喜县东官庄大队用品种石庄54和卫东7号;1978年在太谷本校农场用品种晋麦8号和农大139,并结合对不同株型长相的30个国内外引种的材料,在苗期、分孽—孕穗期和抽穗后等不同时期进行叶片面积的测量。用投影求积法总共计算了两万余张叶片的面积。每次测量的样本是用随机取样20株,分别求出各粟位和各叶位的叶片面积。按调查日期计算出单株总叶面积及不同叶位的叶片面积与相应单株叶面积的相关系数;求出最大叶片面积与单株叶面积的函数关系;按不同叶数时期,计算叶面积的回归方程,做为估算总叶片面积的模式。
结果及讨论
一、分蘖对单株叶面积的影响
小麦单株叶面积受单株分孽数目和各蘖上的叶片面积的影响。分蘖数目的多少对单株叶面积大小的影响是显而易见的。因此在估算单株叶面积时,首先需要了解不同蘖位上叶片面积的差异规律。三年测量的结果见表1。
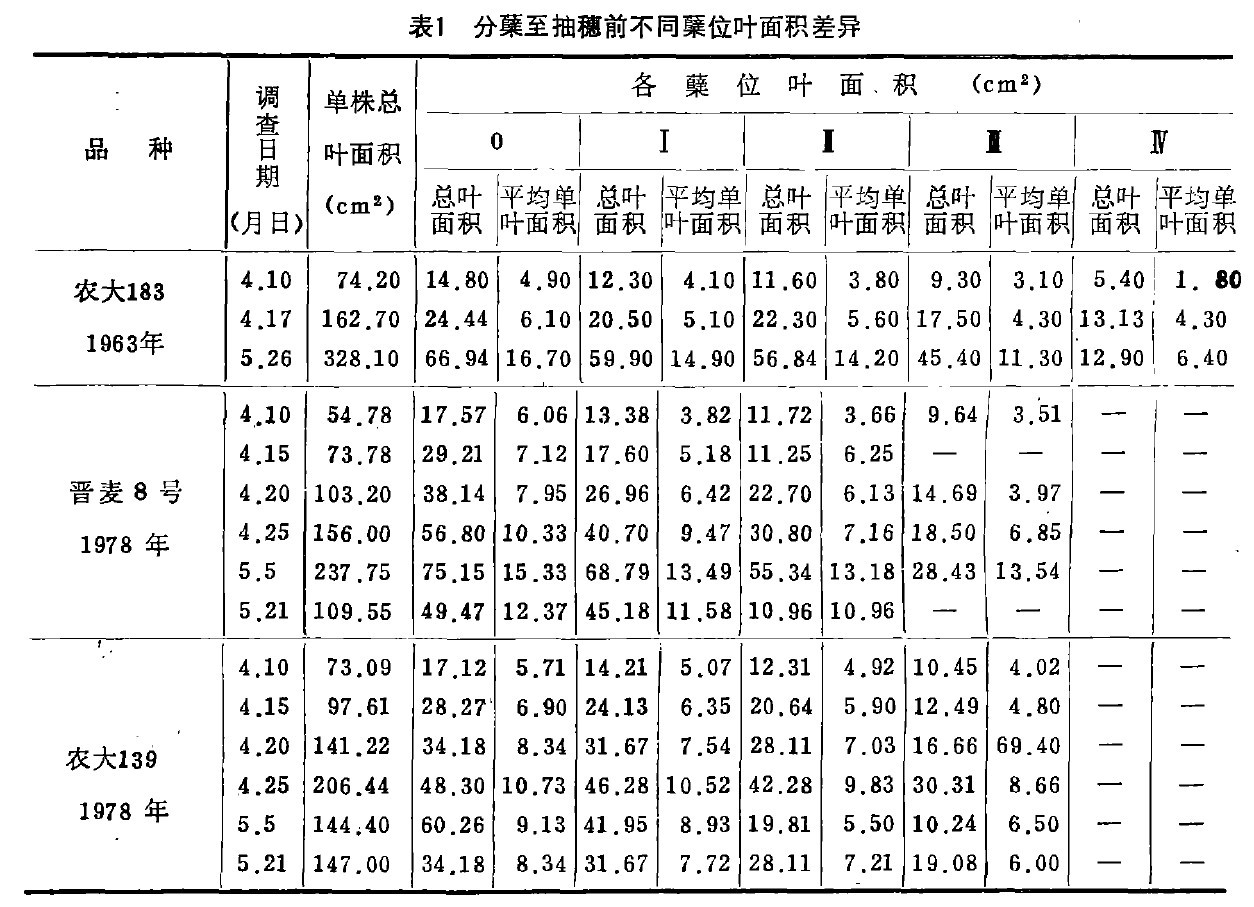
表中可以看出分蘖对单株叶面积的影响是随着蘖位的增高,各孽蘖位的叶面积,无论是总面积或平均单叶面积都相应降低。这项结果给我们提出了在估算叶面积时,如何确定蘖位来采取叶样的问题。因此,需要进一步了解同一蘖位上不同叶位的叶面积的变异规律。
二、各戴位不同部位叶面积的变异
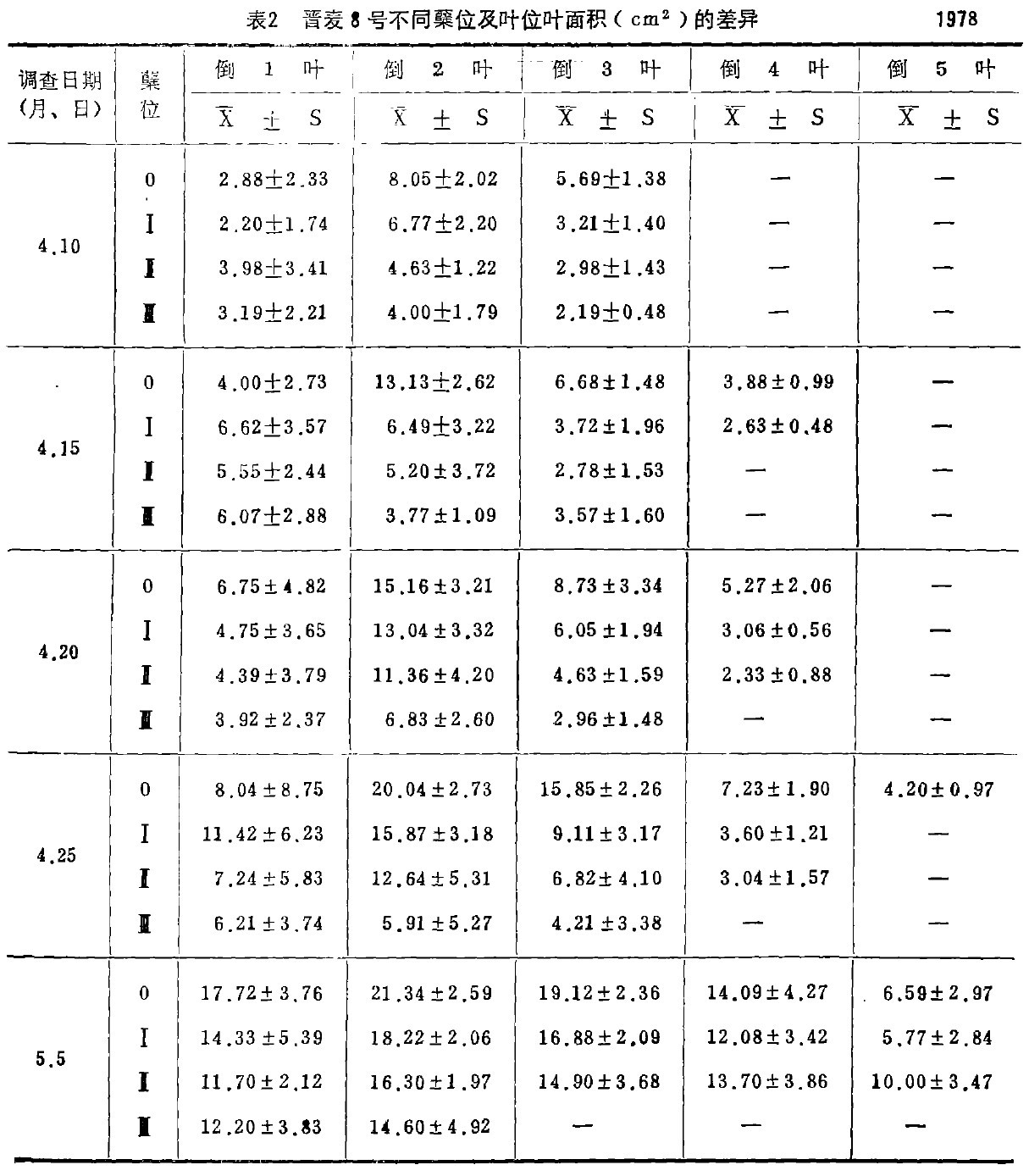
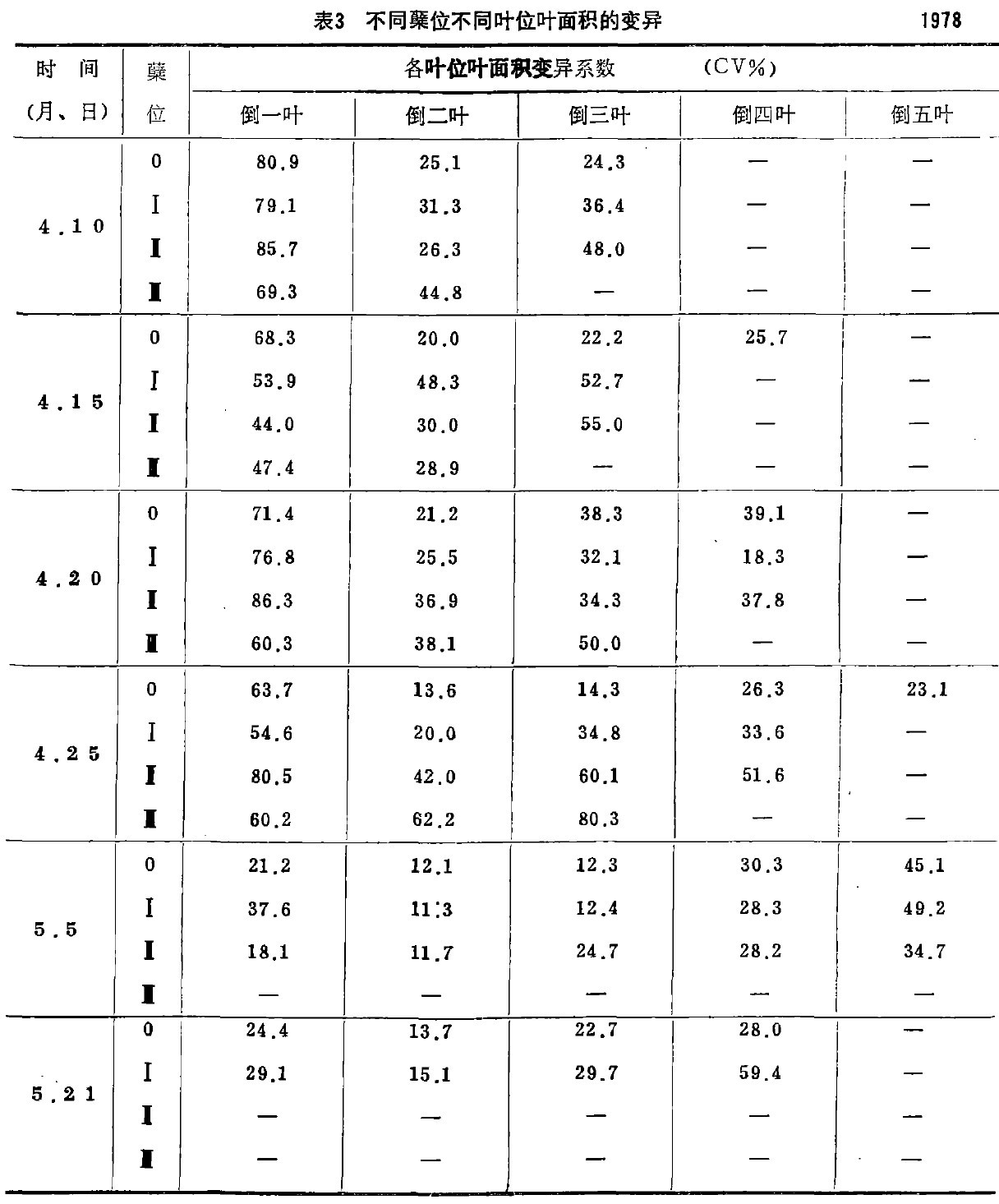
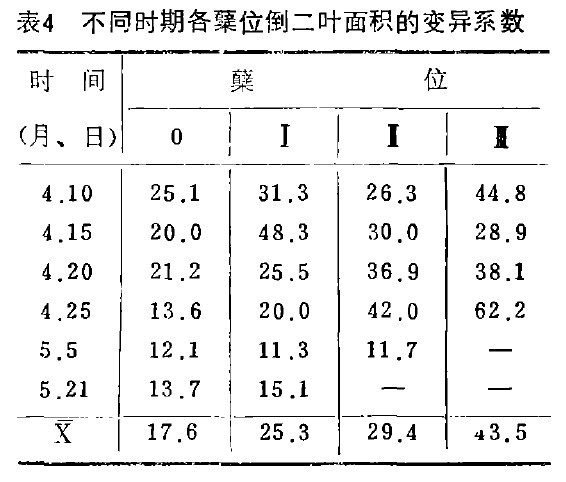
综合表3和表4,可以明确主茎上倒第二汁片是最大的叶片,也是面积相对稳定的叶片。
三、不同叶位的叶面积与单株叶面积的相关性
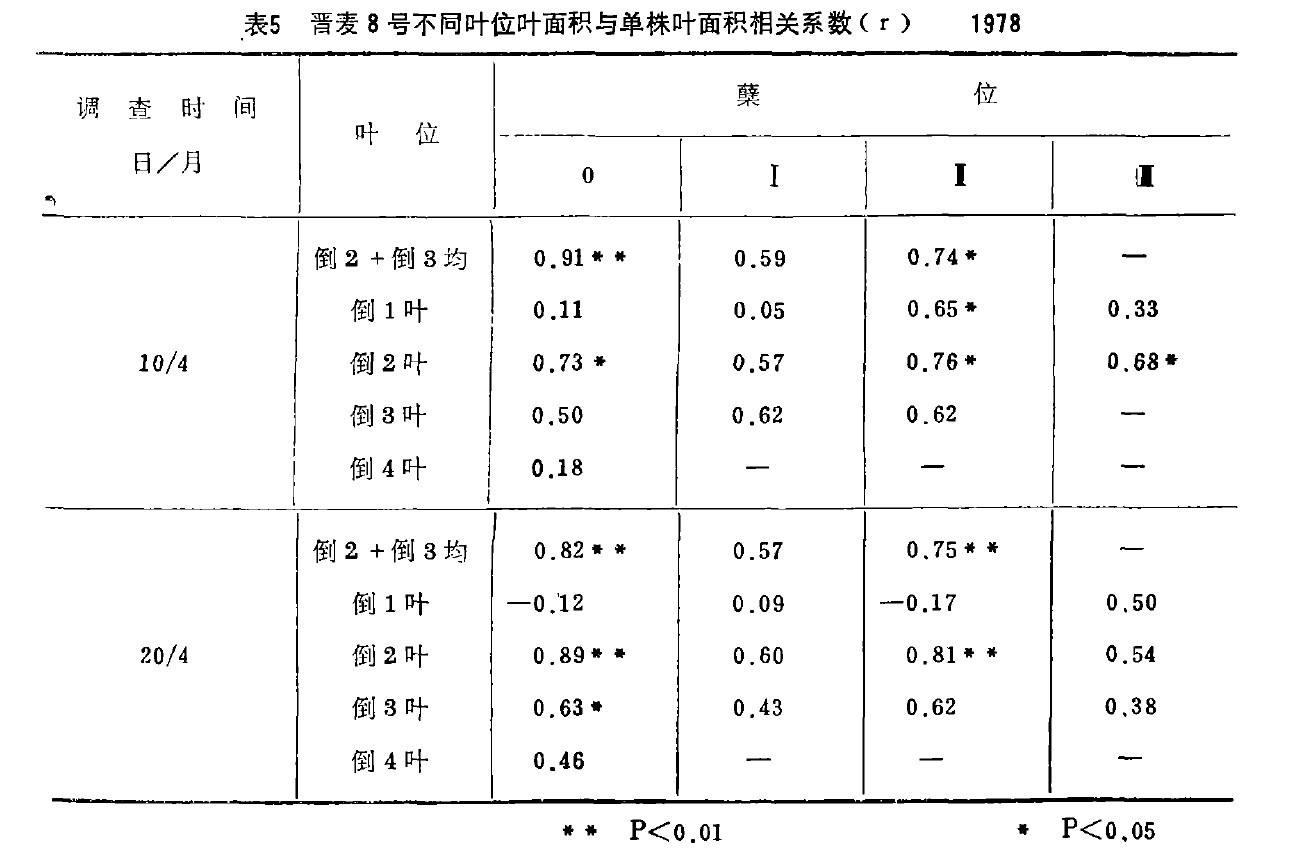
由于主茎倒二叶的叶面积是相对稳定的,导致我们设想能否用它做为“标准叶片”来估算单株的叶面积。因此,计算了不同叶位叶面积与单株叶面积的相关系数r(表5)。
以表中四月十日的调查资料的相关系数为例,可以看到,虽然各孽位倒第二叶与单株叶面积的相关系数都较高(X0.5 ),但值得注意的是主茎倒2,3两叶的叶面积平均值与单株叶面积的相关系数在两个时期先后达r=0.91和r二o.8z,(P
四、主茎倒2、3两叶和其它叶片面积的关系
主茎倒2,3叶是各时期单株最大的两个叶片,用它们估计单株叶面积必然大于实际叶面积,因此需要加以校正。为了校正应先找出它们之间的数量关系。最简单的方法是找出用倒2,3两叶平均值估算的叶面积(Ae)和实测叶面积(AP)的比值(K),即
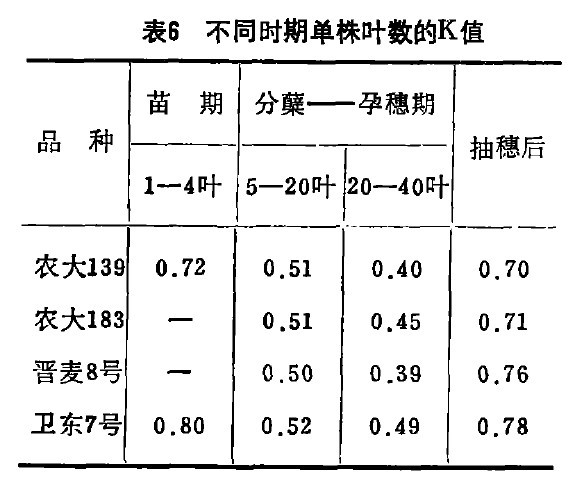
由上式看出,当AP=Ae时,K=1。当Ae>AP时,K<1。当AP 1。据大量观察,小麦不同时期K值不同。幼苗期由于叶片数目少,叶片差异小,因而AP和Ae的的比值近于1。说明二者差异较小。开始分孽后,随着分孽的增加,单株叶数亦增加,Ae相应增大,因而K值由大变小,Ae与AP差异变大。抽穗后,无效分孽死亡,成穗叶面积以单茎计算,单茎上叶面积差异变小,因而K值又加大,表明Ae与AP差异又缩小,上述规律不同品种表现变化趋势基本一致(表6)。
虽然两者关系在趋势上基本一致,但在确切的数量关系上,我们发现并不紧密,因此用K做为系数来估算叶面积还不适用。
五、不同叶数时期的叶面积回归方程
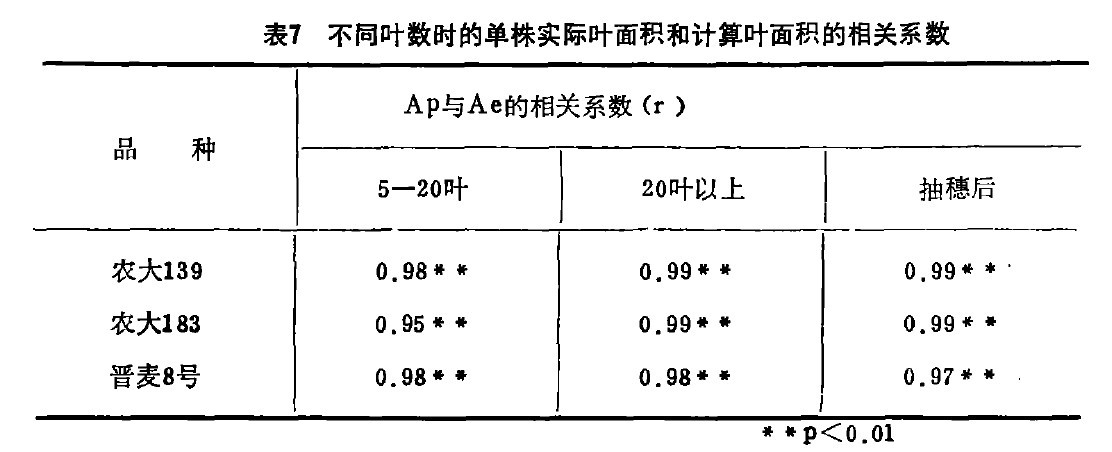
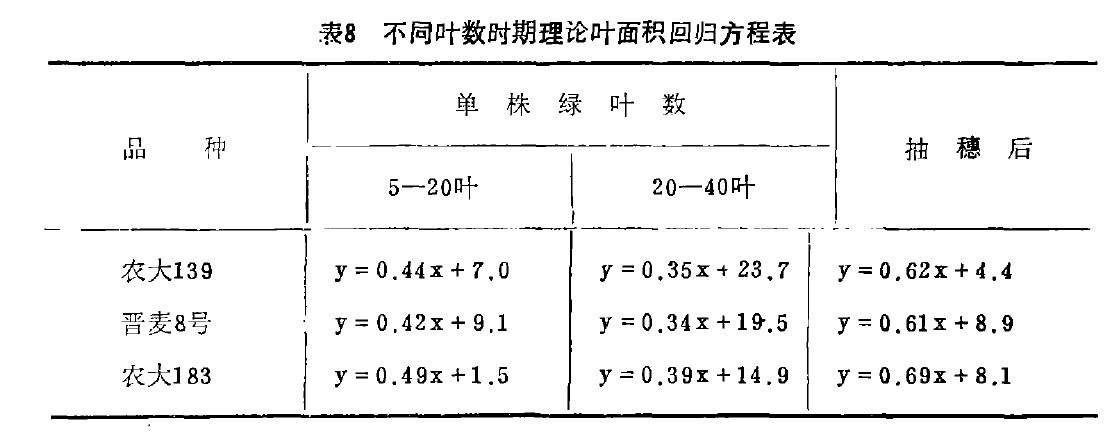
根据不同叶数时期单株计算叶面积A(Ae=主茎倒2,3叶平均叶面积x单株古.片数)和实际叶面积Ap的相关程度(表7)看出,利用主茎倒2,3叶计算所得的单株叶面积和实际叶面积的相关系数(r),都达到0,9以上,说明两者具有高度相关关系。
为了求得不同时期Ae与AP严密的数量关系又计算了不同时期回归方程(表8)进一步测定品种间各回归方程的差异显著性看出:


为了检验用上列回归方程计算叶面积的可靠性,我们用表8所列品种,分别于三个时期各随机选取20株,表明理论计算数值和实测数值相符,回归方程均可成立。
为了进一步检验上述回归方程式的应用范围又对部分播种较稀,单株营养面积很大的原始材料在叶面积变异最大的孕穗前后进行了 Xz检验,共计检验15个品种其中Xz检验适合和高度适合者有六个品种,共计有农林77,农林71和农林54。不适合的有9个品种。原因又分两种情况。
1.理论值>实际值:这类品种大多是分孽力强,在单株营养面积较大的情况下,孕穗前单株绿叶数可达40叶以上,而且单株各叶片大小不整齐,属于这一类的品种如Purkof,腾交等。对这类品种叶面积求算所得的理论叶面积再乘以(1—7/100)即理论值x(11—7/100),仍可适用。
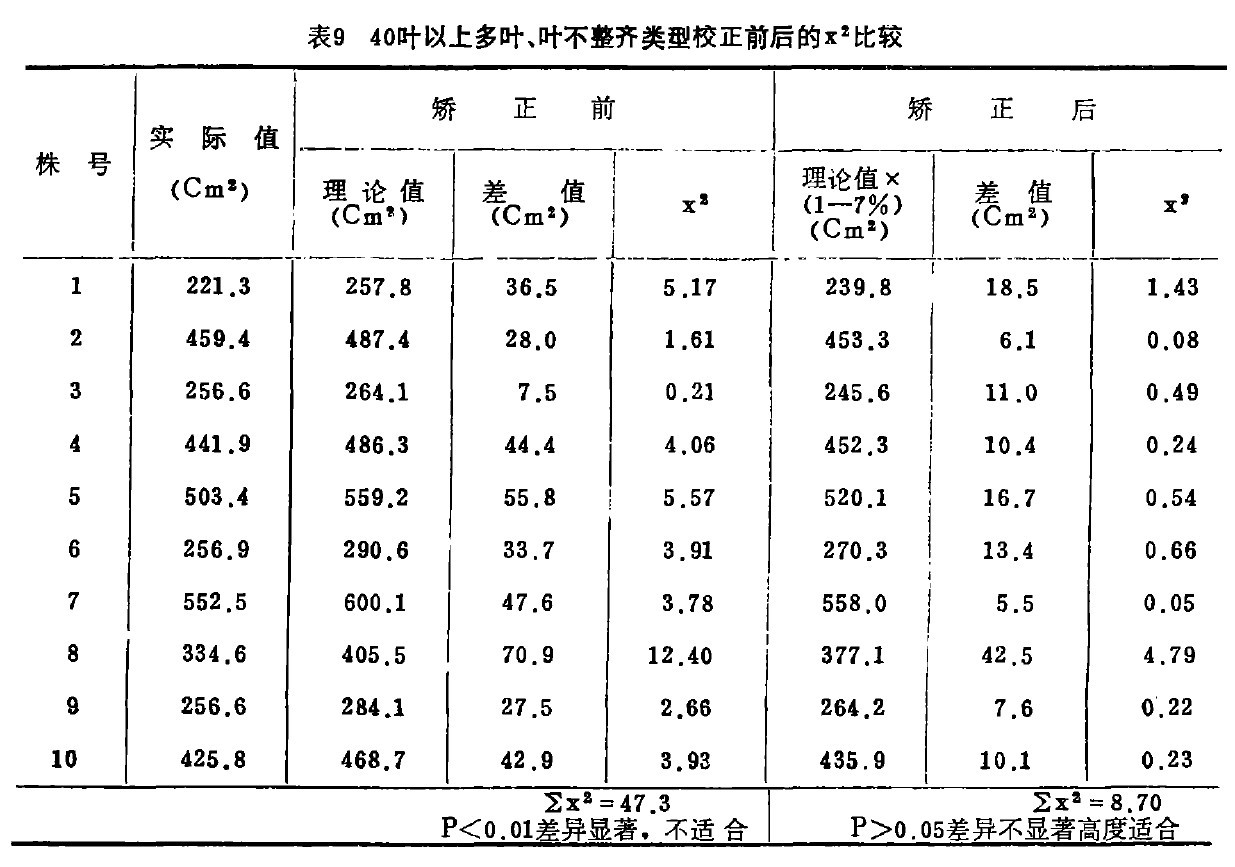
表9是这类品种植株校正前后的Xz比较。
2.理论值<实际值:这类品种特点是分孽力强,单株绿叶数在孕穗前达到35叶以上.,并且叶大而整齐,最大标准叶片在25-30cmz以上,属于这类品如洛夫林,山前,阿夫乐尔,巴那特卡等。对这类品种叶面积求算所查得的理论叶面积再乘以(1+ 15,即:理论值x(1+15/100),亦可适用。
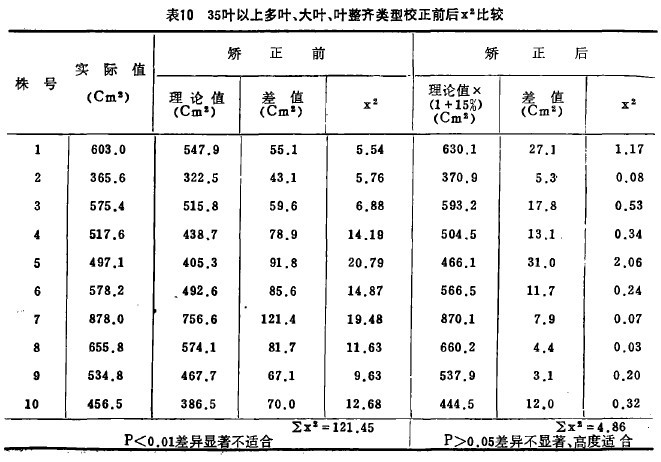
表10是这类品种叶面积较正前后与实际叶面积X2测定的比较。
根据以上得出的回归方程式,再加以校正可以编制出《小麦叶面积查算表》,便于在研究工作中使用。




